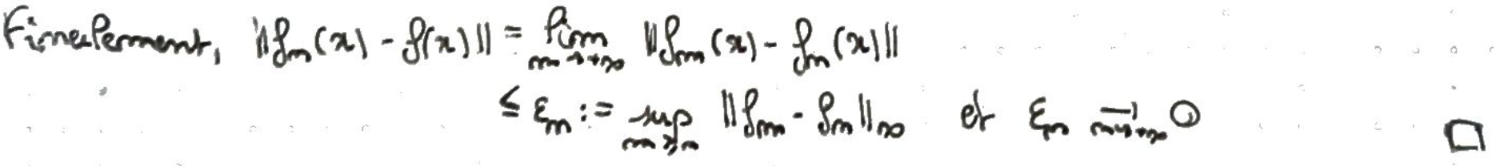Montrer que si \(E\) est un Banach, alors toute suite absolument convergente est convergente.

La suite des sommes partielles est de Cauchy (via \(\ne\triangle\)), donc converge.

Montrer que si un evn est tel que toute série normalement convergente est convergente, alors c'est un Banach.

A partir d'une suite de Cauchy, on construit une sous-suite dont la distance entre les termes consécutifs peuvent être majorés par \(\frac1{2^k}\).

La série des normes de termes consécutifs est donc normalement convergente.

On utilise l'hypothèse pour obtenir une somme télescopique qui converge, ce qui prouve la convergence de la suite (car pour une suite de Cauchy, la convergence d'une sous-suite est une hypothèse suffisante de la convergence.)

Montrer que si \(E\) est un evn et \(F\) un Banach, alors \(L(E,F)\) est un Banach pour la Norme induite.

On utilise une propriété de majoration de norme d'opérateurs pour construire la limite point par point.

La limite est linéaire par continuité de l'addition et de la multiplication par un scalaire.

On a aussi une majoration de la norme, ce qui montre que la limite est continue.

On montre que la convergence a bien lieu pour la norme induite en passant au \(\sup_{x\in B^\prime_E(0,1)}\) dans la norme.

Montrer que si \((X,\mathcal U)\) est un espace topologique, et si \(E\) est un Banach, alors \(\mathcal C_b^0(X,E)\) est un Banach pour \(\lVert\cdot\rVert_\infty\).

Construction point par point de la limite.

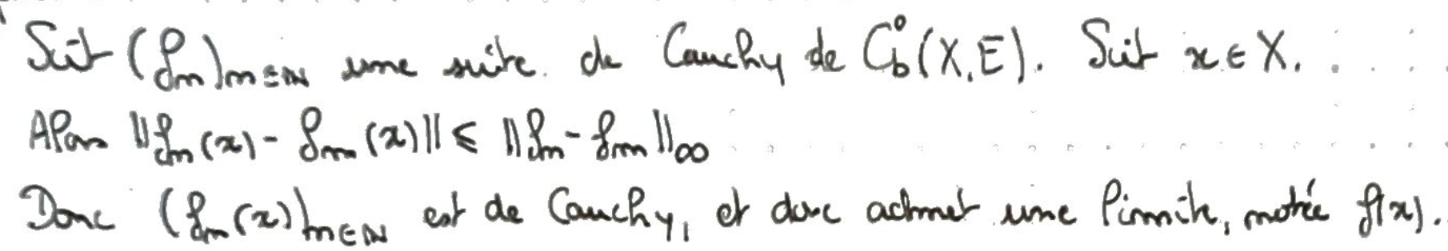
La limite est bornée via une majoration de la norme.

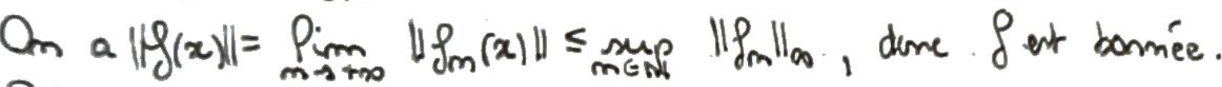
On montre que la limite est continue en montrant que les images d'éléments proches sont proches (via des boules).

On conclut en montrant que la convergence a bien lieu avec la norme \(\lVert\cdot\rVert_\infty\).

Démontrer la proposition suivante :

Construction de la limite via la norme \(\lVert\cdot\rVert_\infty\).

On montre que l'autre partie de la norme est finie.

On montre que la convergence a bien lieu pour la bonne norme.

Démontrer la proposition suivante :

Construction de limites de chacun des termes participant au \(\max\) via la limite uniforme.

Pour conclure, on doit montrer que chaque limite est \(\mathcal C^1\) et que dériver par rapport à un vecteur de la base canonique conserve le fait d'être une limite.

On fait cela en utilisant le théorème fondamental d'analyse et en passant par la convergence uniforme.